A. Persamaan Umum Kurva Berderajat Dua
Persamaan Umum :
persamaan umum diatas dimana koefisien A dan B keduanya tidak boleh 0.
esentrisitas :
e = d ; d' sehingga e ; d / d'
e = 1 jika d = d'
e < 1 jika d / d' < 1 sehingga d < d'
e > 1 jika d / d' > 1 sehingga d > d'
Contoh sebuah kurva berderajat dua adalah irisan kerucut sehingga membentuk sebuah lingkaran.
Lingkaran
lingkaran merupakan himpunan titik titik yang jaraknya terhadap titik tertentu sama panjang.
misal , lingkaran berpusat di (0,0) berjari jari 3 melalui titik titik :
(3,0) = 9A + 3 D + F = 0
(0,3) = 9B + 3E + F = 0
(-3,0) = 9A - 3D + F = 0
(0,-3) = 9B - 3E + F = 0
[ persamaan diatas menggunakan persaman kurva berderajat 2]
kemudian , persamaan yang diketahui kita eliminasikan sebagai berikut :
untuk nilai c maka
titik ( 5/2 , 5/3 ) :
Ataupun dengan cara yang mudah yaitu :
menggunakan konsep jarak :
\
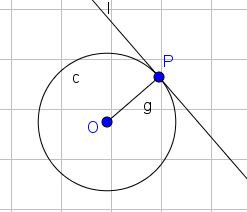
Garis Singgung ( Tangent ) Lingkaran
ket :
OP = jari jari lingkaran
l = garis singgung p ( garis singgung tegak lurus terhadap jari jari )
Garis Singgung Antara Dua Lingkaran
1. Garis Singgung Persekutuan Dalam
garis singgung persekutuan dalam adalah garis singgung yang menyinggung dua lingkaran dan memotong garis yang menghubungkan titik pusat.
seperti berikut :
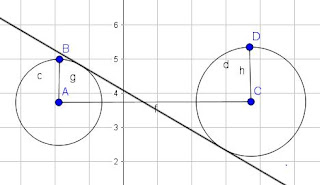
2. Garis Singgung Persekutuan Luar
garis singgung persekutuan luar adalah garis singgung yang menyinggung dua lingkaran dan tidak memotong garis yang menghubungan kedua titik pusat lingkaran.
contoh :

















Tidak ada komentar:
Posting Komentar